Ondas
En física una onda consiste en la propagación de una perturbación de alguna propiedad de un medio, por ejemplo, densidad, presión, campo eléctrico o campo magnético, a través de dicho medio, implicando un transporte de energía sin transporte de materia. El medio perturbado puede ser de naturaleza diversa como aire , agua , un trozo de metal e, incluso, inmaterial como el vació.
Longitud de onda
La longitud de onda es el período espacial o la distancia que hay de pulso a pulso. Normalmente se consideran 2 puntos consecutivos que poseen la misma fase: 2 máximos, 2 mínimos, 2 cruces por cero.
Periodo
En física , el periodo de una oscilación u onda (T) es el tiempo transcurrido entre dos puntos equivalentes de la onda. El concepto aparece tanto en matemáticas como en física y otras áreas de conocimiento.
Ondas longitudinales
Una onda longitudinal es una onda en la que el movimiento de oscilación de las partículas del medio es paralelo a la dirección de propagación de la onda. Las ondas longitudinales reciben también el nombre de ondas de presión u ondas de compresión. Algunos ejemplos de ondas longitudinales son el sonida y las ondas tipo sísmicas o generadas en un terremoto.
Ondas mecánicas
Una onda mecánica es una perturbación de las propiedades mecánicas de un medio material (posición, velocidad y energía de sus átomos o moléculas) que se propaga en el medio.
Todas las ondas mecánicas requieren:
- Alguna fuente que cree la perturbación.
- Un medio en el que se propague la perturbación.
- Algún medio físico a través del cual elementos del medio puedan influir uno al otro.
En un medio elástico no sometido a fuerzas volumétricas la ecuación de movimiento de una onda elástica que relaciona la velocidad de propagación con las tensiones existentes en el medio elástico vienen dadas, usando el convenio de sumación de Einstein, por:
(1)
Donde  es la densidad y el término entre paréntesis del segundo término coincide con la aceleración o derivada segunda del desplazamiento. Reescribiendo la ecuación anterior en términos de los desplazamientos producidos por la onda elástica, mediante las ecuaciones de Lamé-Hooke y las relaciones del tensor deformación con el vector desplazamiento, tenemos:
es la densidad y el término entre paréntesis del segundo término coincide con la aceleración o derivada segunda del desplazamiento. Reescribiendo la ecuación anterior en términos de los desplazamientos producidos por la onda elástica, mediante las ecuaciones de Lamé-Hooke y las relaciones del tensor deformación con el vector desplazamiento, tenemos:
 es la densidad y el término entre paréntesis del segundo término coincide con la aceleración o derivada segunda del desplazamiento. Reescribiendo la ecuación anterior en términos de los desplazamientos producidos por la onda elástica, mediante las ecuaciones de Lamé-Hooke y las relaciones del tensor deformación con el vector desplazamiento, tenemos:
es la densidad y el término entre paréntesis del segundo término coincide con la aceleración o derivada segunda del desplazamiento. Reescribiendo la ecuación anterior en términos de los desplazamientos producidos por la onda elástica, mediante las ecuaciones de Lamé-Hooke y las relaciones del tensor deformación con el vector desplazamiento, tenemos:(2a)
Que escrita en la forma vectorial convencional resulta:
(2b)
Ecuación de la onda
La ecuación de la onda es una importante ecuación diferencial en derivadas parciales lineal de segundo orden que describe la propagación de una variedad de ondas , como las ondas sonoras , las ondas de luz y las ondas en el agua. Es importante en varios campos como la acústica , el electromagnetismo y la dinámica de fluidos .
La ecuación de onda es el ejemplo prototipo de una ecuación diferencial parcial hiperbólica . En su forma más elemental, la ecuación de onda hace referencia a una función u(x,t) que satisface:
Reflexión de una onda sonora
Reflexión se refiere al fenómeno por el cual una onda se absorbe o regresa.
Refracción de sonido
La refracción es el cambio de dirección que experimenta una onda al pasar de un medio a otro. Sólo se produce si la onda incide oblicuamente sobre la superficie de separación de los dos medios y si éstos tienen índices de refracción distintos.
Difracción de la onda
La difracción es un fenómeno que afecta a la propagación de la onda. Hablamos de difracción cuando el sonido en lugar de seguir en la dirección normal, se dispersa en una continua dirección.
La difracción se puede producir por dos motivos diferentes:
- porque una onda sonora encuentra a su paso un pequeño obstáculo y lo rodea. Las bajas frecuencias son más capaces de rodear los obstáculos que las altas. Esto es posible porque las longitudes de onda en el espectro audible están entre 1,7cm y 17m, por lo que son lo suficientemente grandes para superar la mayor parte de los obstáculos que encuentran.
- porque una onda sonora topa con un pequeño agujero y lo atraviesa.
Interferencia de la onda
En física , la interferencia es un fenómeno en el que dos o más ondas se superponen para formar una onda resultante de mayor o menor amplitud.
En la superposición de ondas con la misma frecuencia el resultado depende de la diferencia de fase . Si sumamos dos ondas
. Si sumamos dos ondas  y
y  , la onda resultante tendrá la misma frecuencia y amplitud
, la onda resultante tendrá la misma frecuencia y amplitud 
En la superposición de ondas con la misma frecuencia el resultado depende de la diferencia de fase
 . Si sumamos dos ondas
. Si sumamos dos ondas  y
y  , la onda resultante tendrá la misma frecuencia y amplitud
, la onda resultante tendrá la misma frecuencia y amplitud 
Sonido
El sonido , en física, es cualquier fenómeno que involucre la propagación en forma de ondas elásticas (sean audibles o no), generalmente a través de un fluido (u otro medio elástico) que esté generando el movimiento vibratorio de un cuerpo
Características del sonido
Desde un punto de vista físico el sonido es una vibración que se propaga en un medio elástico. Para que se produzca sonido se requiere la existencia de un cuerpo vibrante, denominado foco (cuerda tensa, varilla, una lengüeta) y de un medio elástico que transmita esas vibraciones, que se propagan por él constituyendo lo que se denomina onda sonora.
La intensidad del sonido se define como la la potencia acústica transferida por una onda sonora por unidad del área normal a la dirección de propagación.
 ;
;- El tono es la sensación auditiva o atributo psicológicos de los sonido que los caracteriza como más agudos o más graves, en función de la propiedad física llamada frecuencia
Efecto doppler
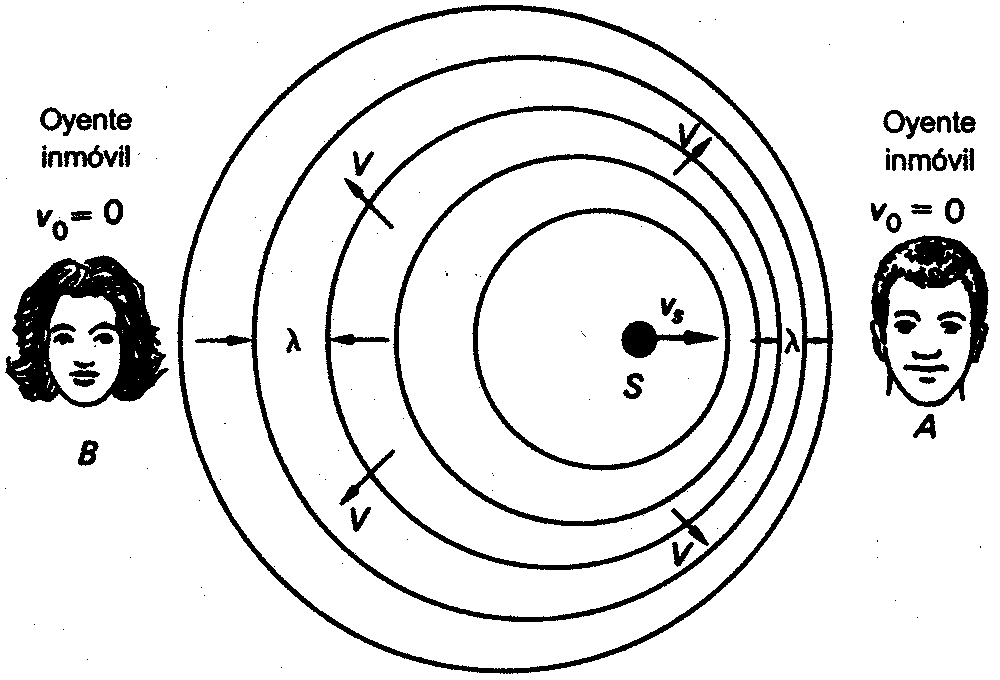
El efecto dopplet , llamado así por el físico austriaco Christian Andreas Doppler, es el aparente cambio de frecuencia de una onda producida por el movimiento relativo de la fuente respecto a su observador. Doppler propuso este efecto en 1842 en su tratado Über das farbige Licht der Doppelsterne und einige andere Gestirne des Himmels (Sobre el color de la luz en estrellas binarias y otros astros).
Imaginemos que un observador O se mueve con una velocidad  que tiene una dirección y sentido hacia una fuente de sonido S que se encuentra en reposo. El medio es aire y también se encuentra en reposo. La fuente emite un sonido de velocidad V, frecuencia
que tiene una dirección y sentido hacia una fuente de sonido S que se encuentra en reposo. El medio es aire y también se encuentra en reposo. La fuente emite un sonido de velocidad V, frecuencia  y longitud de onda
y longitud de onda 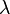 . Por lo tanto, la velocidad de las ondas respecto del observador no será
. Por lo tanto, la velocidad de las ondas respecto del observador no será  , sino la siguiente:
, sino la siguiente:
 que tiene una dirección y sentido hacia una fuente de sonido S que se encuentra en reposo. El medio es aire y también se encuentra en reposo. La fuente emite un sonido de velocidad V, frecuencia
que tiene una dirección y sentido hacia una fuente de sonido S que se encuentra en reposo. El medio es aire y también se encuentra en reposo. La fuente emite un sonido de velocidad V, frecuencia  y longitud de onda
y longitud de onda 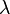 . Por lo tanto, la velocidad de las ondas respecto del observador no será
. Por lo tanto, la velocidad de las ondas respecto del observador no será  , sino la siguiente:
, sino la siguiente:
Sin embargo, no debemos olvidar que como la velocidad del medio no cambia, la longitud de onda será la misma, por lo tanto, si:

Pero como mencionamos en la primera explicación, el observador al acercarse a la fuente oirá un sonido más agudo, esto implica que su frecuencia es mayor. A esta frecuencia mayor captada por el observador se la denomina frecuencia aparente, que la denominamos f'.

El observador escuchará un sonido de mayor frecuencia debido a que 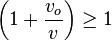
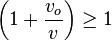
Tubos sonoros
| Los tubos de caña o de otras plantas de tronco hueco, constituyeron los primeros instrumentos musicales. Emitían sonido soplando por un extremo. El aire contenido en el tubo entraba en vibración emitiendo un sonido.Si un tubo es abierto, el aire vibra con su máxima amplitud en los extremos. En la figura, se representan los tres primeros modos de vibración Como la distancia entre dos nodos o entre dos vientres es media longitud de onda. Si la longitud del tubo es L, tenemos que L=l /2, L=l , L=3l /2, ... en general L=nl /2, n=1, 2, 3... es un número entero Considerando que l =vs/f (velocidad del sonido dividido la frecuencia). Si el tubo es cerrado se origina un vientre en el extremo por donde penetra el aire y un nodo en el extremo cerrado. Como la distancia entre un vientre y un nodo consecutivo es l /4. La longitud L del tubo es en las figuras representadas es L=l /4, L=3l /4, L=5l /4... En general L=(2n+1) l /4; con n=0, 1, 2, 3, ... Las frecuencias de los distintos modos de vibración responden a la fórmula Cuerdas vibrantes
La vibración de una cuerda es una onda . Por lo general una cuerda vibrante produce un sonido cuya frecuencia en la mayoría de los casos es constante. Por lo tanto, dado que la frecuencia caracteriza la altura , el sonido producido es una nota constante. Las cuerdas vibrantes son la base de todos los instrumentos de cuerdas tales como la guitarra , el violín o el piano.
Sea
 la longitud de un trozo de cuerda, la longitud de un trozo de cuerda,  su masa, y su masa, y  sudensidad lineal. Si la componente horizontal de la tensión sobre la cuerda es constante, sudensidad lineal. Si la componente horizontal de la tensión sobre la cuerda es constante,  , entonces la tensión que actúa en cada extremo del trozo de cuerda se expresa como , entonces la tensión que actúa en cada extremo del trozo de cuerda se expresa como
Si ambos ángulos son pequeños, entonces las tensiones en cada extremo son iguales y la fuerza neta horizontal es nula. Aplicando la segunda Ley de Newton para la componente vertical, la masa de este trozo multiplicada por su aceleración,
 , será igual a la fuerza neta ejercida sobre el trozo de cuerda: , será igual a la fuerza neta ejercida sobre el trozo de cuerda:
Dividiendo esta expresión por
 y substituyendo la primera y la segunda ecuación resulta y substituyendo la primera y la segunda ecuación resulta
Las tangentes de los ángulos en los extremos del trozo de cuerda son iguales a las pendientes en los extremos, con un signo negativo adicional a causa de la definición de beta. Con este dato y re ordenando se obtiene
En el límite cuando
 tiende a cero, el lado izquierdo de la igualdad es la definición de la derivada segunda de tiende a cero, el lado izquierdo de la igualdad es la definición de la derivada segunda de  : :
Esta es la ecuación de onda para
 , y el coeficiente de la derivada segunda en el tiempo es , y el coeficiente de la derivada segunda en el tiempo es  ; por lo tanto ; por lo tanto
donde
 es la velocidad de propagación de la onda en la cuerda. (véase el artículo sobre la ecuación de onda para mayores detalles). Sin embargo, este desarrollo es solo válido para vibraciones de amplitud pequeña; en el caso de amplitudes grandes, es la velocidad de propagación de la onda en la cuerda. (véase el artículo sobre la ecuación de onda para mayores detalles). Sin embargo, este desarrollo es solo válido para vibraciones de amplitud pequeña; en el caso de amplitudes grandes,  no es una buen aproximación de la longitud del trozo de cuerda, la componente horizontal de la tensión no es necesariamente constante, y no es correcto aproximar las tensiones horizontales con no es una buen aproximación de la longitud del trozo de cuerda, la componente horizontal de la tensión no es necesariamente constante, y no es correcto aproximar las tensiones horizontales con  . .
Aquí una breve demostración de como cada material produce un nivel sonoro diferente a otro.
|




















No hay comentarios:
Publicar un comentario